Given a directed acyclic graph, with n vertices numbered from 0 to n-1, and an array edges where edges[i] = [fromi, toi] represents a directed edge from node fromi to node toi.
Find the smallest set of vertices from which all nodes in the graph are reachable. It's guaranteed that a unique solution exists.
Notice that you can return the vertices in any order.
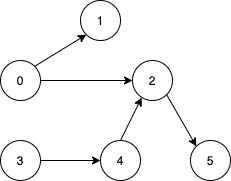
Input: n = 6, edges = [[0,1],[0,2],[2,5],[3,4],[4,2]] Output: [0,3] Explanation: It's not possible to reach all the nodes from a single vertex. From 0 we can reach [0,1,2,5]. From 3 we can reach [3,4,2,5]. So we output [0,3].
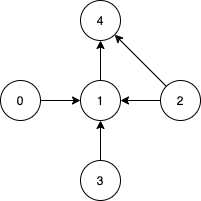
Input: n = 5, edges = [[0,1],[2,1],[3,1],[1,4],[2,4]] Output: [0,2,3] Explanation: Notice that vertices 0, 3 and 2 are not reachable from any other node, so we must include them. Also any of these vertices can reach nodes 1 and 4.
2 <= n <= 10^51 <= edges.length <= min(10^5, n * (n - 1) / 2)edges[i].length == 20 <= fromi, toi < n- All pairs
(fromi, toi)are distinct.
implSolution{pubfnfind_smallest_set_of_vertices(n:i32,edges:Vec<Vec<i32>>) -> Vec<i32>{letmut start = vec![true; n asusize];for edge in edges { start[edge[1]asusize] = false;}(0..n).filter(|&x| start[x asusize]).collect()}}